Один из ключевых рисков, которому подвержены все долговые ценные бумаги является процентный риск, т.е. движение процентных ставок. (О снижении процентного риска в статье Хеджирование процентного риска облигации). Дюрация отражает величину процентного риска или чувствительность цены облигации к изменению процентных ставок. Рассмотрим две облигации:
1) погашение через 5 лет, купон 5%
2) погашение через 10 лет, купон 10%
Из двух бумаг трудно определить, какая в большей степени подвержена процентному риску. Первая облигация платит меньший купон (что увеличивает процентный риск), в то время как вторая погашается на 5 лет позже (что также увеличивает процентный риск). Поэтому необходим такой показатель, который бы объединил оба фактора: купонную ставку и срок погашения, и позволил сравнить процентные риски облигаций с разными критериями. Таким показателем и является дюрация.
Дюрация Маколея (Maccaulay duration)
В 1938 году Фредерик Маколей изобрел самый первый вид дюрации. Дюрация Маколея – это средневзвешенное время до получения купонов и номинала, где вес определяется как доля текущего значения денежного потока от цены облигации. Таким образом, дюрация Маколея измеряется в годах.
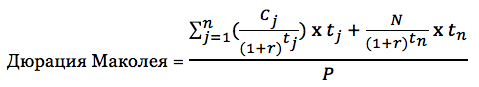
C – купонный платеж в денежном выражении
r – доходность облигации (YTM или YTC)
t – время поступления выплаты (купона или номинала)
N – номинал облигации в денежном выражении
P – текущая цена облигации
|
Пример 1: обыкновенная облигация Посчитаем дюрацию облигации, которая торгуется по номиналу и имеет три года до погашения. Купон равен 9% годовых и платится в конце каждого года. В связи с тем, что цена облигации равна 100, доходность к погашению составляет 9%. |
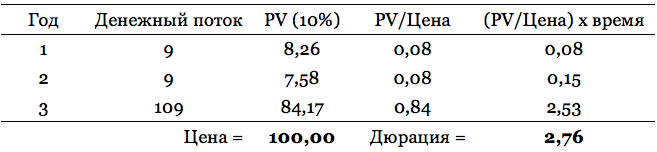
Что это означает? Несмотря на то, что облигация погашается через 3 года, ее чувствительность к движению процентных ставок меньше, чем у трехгодовой бескупонной облигации из-за купонных выплат. В связи с тем, что облигация платит купоны, которые могут быть переинвестированы, срок инвестирования и процентный риск снижаются. Поэтому, при прочих равных чем выше купон, тем ниже процентный риск, т. е. меньше дюрация.
Расчет дюрации облигации можно представить с помощью точки балансирования на графике. Денежные потоки от облигации (а именно доля текущей стоимости потоков от цены облигации) представляют вес. Дюрация – фактический срок жизни облигации – точка балансирования, измеряемая в годах.

|
Пример 2: (бескупонная облигация) Посчитаем дюрацию бескупонной облигации, которая торгуется по $77,22 и имеет три года до погашения. Доходность к погашению равна 10%. |

Трехлетняя бескупонная облигация с аналогичной доходностью 9% имеет 3 года. Если ставки вырастут, цена бескупонной облигации упадет сильнее в процентном выражении, чем цена купонной облигации. Это связано, с тем, что инвестор получит только одну выплату по истечении 3-х лет, т. е. у него не будет промежуточных средств (купонов), которые он бы мог переинвестировать под более высокие ставки. В то время как владелец 9% купонной облигации с погашением также через 3 года сможет вкладывать получаемые купоны под более высокие рыночные ставки, что снижает процентный риск (дюрация бумаги сокращается до 2,76 года).
И наоборот, в случае снижения ставок центральным банком цена бескупонной облигации вырастет больше, чем цена купонной из-за реинвестирования: получаемые купоны будут вложены по более низким ставкам.
Упрощенное математическое определение дюрации и конвекции, а также их взаимосвязь описаны в "Математическое описание дюрации и конвекции". Расчет дюрации долговой ценной бумаги в торговых терминалах (в том числе Bloomberg) строится по этим формулам.
Правило: Дюрация Маколея для всех бескупонных облигаций всегда равна сроку до погашения.

Модифицированная дюрация
Модифицированная дюрация является общепринятым показателем процентного риска долговой ценной бумаги, так как она отражает, на сколько изменится цена облигации при изменении процентных ставок на 1%.
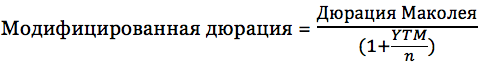
YTM – доходность к погашению
n – количество купонных платежей в год
|
Пример 3. Определим модифицированную дюрацию 9% купонной облигации с датой погашения через 3 года. Бумага торгуется по номиналу и имеет доходность 9% годовых. Купоны платятся в конце года. |
Исходя из предыдущих расчетов, дюрация Маколея этой облигации составляет 2,76 года. Поэтому:
Модифицированная дюрация = 2,76/(1 + 0,09) = 2,531%
Это означает, что при росте (падении) доходности облигации на 1% или 100 базисных пунктов, цена облигации снизится (вырастет) на 2,531%. Отметим, если облигация платит купоны два раза в год, то необходимо поделить доходность в знаменателе на 2.
Хеджирование дюрации (процентного риска) является неотъемлемой частью управления облигационным портфелем. Методы хеджирования, потенциальные риски и примеры описаны в "Хеджирование процентного риска облигации".
Цена одного базисного пункта (price value of basis point, PVBP или DV01)
Используя модифицированную дюрацию, можно посчитать прибыль или убыток от владения облигацией, если доходность изменится на 1 базисный пункт. В английском языке такой показатель называется PVBP (price value of basis point) или DV01 (dollar value of one basis point). Подробнее о расчете и практическом использовании DV01 здесь: Измерение процентного риска портфеля с помощью PV01, PVBP и конвекции.
В случае с 3-х летней облигацией с купоном 9% и рыночной ценой $100, модифицированная дюрация составляет 2,531%. При изменении доходности облигации на 100 базисных пунктов цена облигации изменится на 2,531%. Следовательно, изменение доходности на 1 базисный пункт приведет к изменению цены на
PVBP = ($100 x 2,531%) / 1000 = $0,02531
Рост доходности на 1 базисный пункт приведет к убытку, равному 2,5 центам.
От чего зависит дюрация?
1) размер купона: чем выше купон, тем ниже дюрация
2) срок до погашения: чем дальше дата погашения облигации, тем волатильнее цена облигации, т.е. выше дюрация.
Поэтому, самым низким процентным риском обладают краткосрочные облигации с высокими купонными ставками.
Помимо дюрации, которая является производной 1-го порядка, профессиональные инвесторы в крупных фондах и инвестиционных банках принимают во внимание и конвекцию ценной бумаги. Положительная конвекция (выпуклость цены облигации), характерная для стандартных долговых активов без call feature, ускоряет рост цены облигации при падении доходности и замедляет падение цены – при увеличении доходности. (О расчете конвекции и ее практическом применении в торговле можно прочитать в Конвекция или выпуклость облигации).
