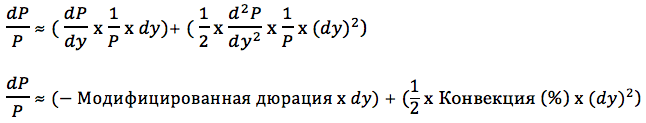Существует математическая связь между ценой обыкновенной облигации и ее доходностью. Цена облигации определяется как:
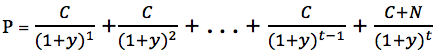
где
P – цена облигации
C – купонная выплата в денежном выражении
y – ставка дисконтирования, при которой цена облигации равна текущей стоимости потоков
N – номинальная стоимость облигации
t – количество периодов до погашения
Периодические купонные платежи (C) и номинал (N) дисконтируются по доходности к погашению (y). Дюрация и конвекция несут за собой расчет изменения цены бумаги, dP, вследствие изменения доходности к погашению, dy. Такой расчет предполагает разложение в ряд Тейлора.
Ряд Тейлора может состоять из нескольких степенных членов в зависимости от требуемой степени точности. Для облигации достаточно первых двух членов:
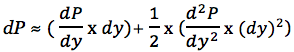
Изменение цены определяется как первая частная производная цены облигации, умноженная на изменение доходности, плюс половина второй частичной производной, умноженной на изменение доходности в квадрате. Первый член уравнения представляет дюрацию, второй является ключевым для определения конвекции.
Дюрация Маколея и Модифицированная дюрация
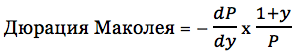
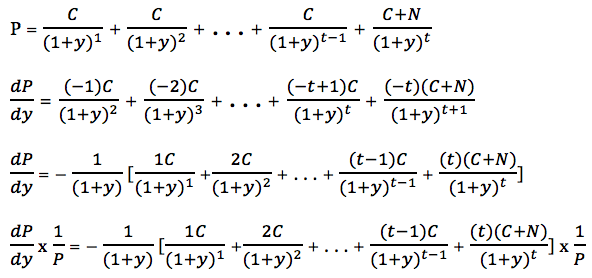

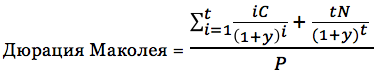
или
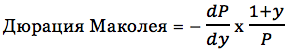
Это выражение было описано канадским экономистом Фредериком Маколеем в его работе о доходностях облигаций США и рынке акций между 1857 и 1936 годами. Знак минус является частью определения дюрации. Первая частная производная имеет отрицательное значение из-за обратной связи между ценой и доходностью. Поэтому знак минус дает дюрации Маколея положительное значение.
Однако профессиональные трейдеры и инвесторы придают большее значение модифицированной дюрации.
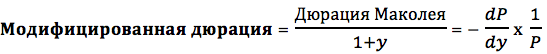
Модифицированная дюрация показывает изменение цены облигации в процентном выражении при движении доходности облигации на один базисный пункт (0,01%) или на один процент (1%).
DV01 = Модифицированная дюрация (0,01%) x P = – dP/dy
Конвекция
Конвекция облигации определяется как 2-ая частная производная.
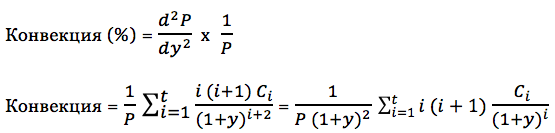
Конвекция в денежном выражении:
Конвекция ($) = Конвекция (%) x P
Вывод