Модель Блэка-Шоулза: формула, условия, примеры

В статье "Бинарное дерево расширение (Часть II)" была построена опционная модель бинарного дерева с 3-мя шагами для опциона колл. Увеличение количества шагов, т.е. уменьшение временного интервала между шагами, приведет к абсолютно аналогичному результату, который можно получить с помощью известной в финансовой сфере модели Блэка-Шоулза. Модель была разработана академиками Блэком, Шоулзом и Мертоном в семидесятых годах двадцатого века и сейчас широко используется как в академической среде, так как в ведущих финансовых корпорациях. Для европейских опционов модель Блэка-Шоулза выглядит следующим образом:

C = SN(d₁) – Xe^-rtN(d₂)

P = Xe^-rtN(–d₂) – SN(–d₁)

 Где:

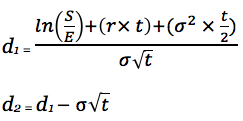
C – стоимость колл опциона

P – стоимость пут опциона

S – спотовая цена базового актива

X – цена страйк опциона

N(d) – функция стандартного нормального распределения

ln(x) - натуральный логарифм с основанием е

 σ – волатильность цены базового актива в годовом выражении

t – время до исполнения опциона, выраженное в годах

r – безрисковая процентная ставка

Формула для колл опциона показывает, что стоимость опциона колл (C) вычисляется как разница между спотовой ценой (S) базового актива и дисконтированной величиной страйка X); значения S и X взвешены с помощью факторов риска N(d₁) и N(d₂). Как и в бинарном методе, формула основана на допуске о том, что 1) опционы можно дельта-захеджировать через торговлю базовым активом, а также 2) класть средства на депозит в банк и брать в кредит по безрисковой процентной ставке. Модель Блэка-Шоулза подразумевает нормальное распределение доходностей базового актива.

Фактор N(d₂) измеряет вероятность, что колл опцион истечет в деньгах и будет исполнен. В то время как фактор N(d₁) является дельтой опциона, т. е. коэффициентом хеджирования. Обычно, функция N(d₂) считает площадь левее значения d₂ под кривой нормального распределения со средним значением 0 и дисперсией 1. Таким образом, N(d₂) вычисляет вероятность, что переменная, имеющая стандартное нормальное распределение будет ниже d₂.

Согласно модели Блэка-Шоулза, стоимость колл опциона составляет:

C = $300 × 0,8721 – $250 × e^{-0,1 x 0,25} × 0,8255 = $60,36

Где:

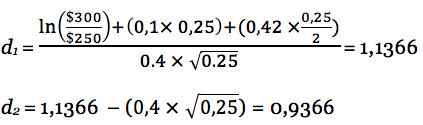
N(d₁) = 0,8721

N(d₂) = 0,8255

Риск-нейтральная вероятность исполнения опциона равна 82,55%, так как опцион изначально находится в деньгах.

Блэк-Шоулз с дивидендами

Модель можно скорректировать под активы, которые платят регулярные дивиденды. Формула, описанная ниже, предполагает, что дивиденды платятся на беспрерывной основе, т. е. отчисляются владельцу базового актива каждую секунду. Обозначим дивидендную доходность буквой q:

C = Se^-qtN(d₁) – Xe^-rtN(d₂)

P = Xe^-rtN(–d₂) – Se^-qtN(–d₁)

Где:

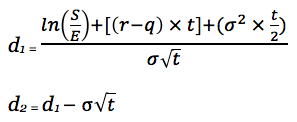
В контексте отдельной акции, предположение о беспрерывой выплате дивидендов является нереалистичным, так как эмитенты обычно платят дивиденды либо раз в год либо каждые полгода. Поэтому, для решения этой проблемы мы можем заменить спотовую цену актива на спотовую цену за вычитанием дисконтированной стоимости дивидендных выплат, ожидаемых в период действия опциона. Дисконтировать дивиденды следует по безрисковой процентной ставке.