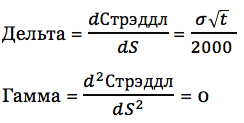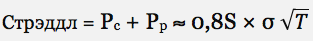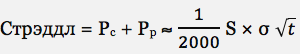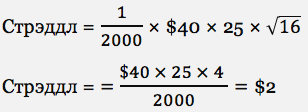Формула для приблизительной стоимости на-деньгах стрэддла (straddle) дает довольно точную оценку рыночной цены ATM стрэддла, учитывая при расчете спотовую цену акций, вмененную волатильность и время до экспирации. Несмотря на то, что это всего лишь приблизительное значение, его достаточно, для того чтобы извлечь другие параметры опционов: греки, сравнить полученное значение с рыночными ценами и принять торговое решение.
ФОРМУЛА СТОИМОСТИ НА-ДЕНЬГАХ СТРЭДДЛА
Стоимость на-деньгах опционов колл и пут можно быстро найти по следующей формуле:
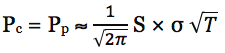
S – спотовая цена актива
σ – вмененная волатильность
T – время до экспирации в годах
Эту формулу можно получить из модели Блэка-Шоулза.
|
Формула стрэддла
Но если рассчитывать время до экспирации в количестве дней, формула примет следующий вид:
|
Предпочтительно использовать количество торговых дней, так как на практике во время реальной торговли легче сказать “10 торговых дней до экспирации”, чем “0.04 лет до экспирации”. Это объясняет, почему константа упала с 0,8 до 1/2000. Аналогичным образом, волатильность часто измеряется в % в годовом выражении. Например, если в среднем стандартное отклонение цены акции составляет 1% в день, волатильность в годовом выражении составляет около 16%.
Эта формула применяется в крупных алгоритмических хедж фондах США и Европы для ускорения расчета опционной стратегии и принятия более быстрого решения.
Обратите внимание, что время до экспирации и вмененная волатильность должны быть одинаковым для опционов колл и пут.
|
Пример. Какая цена на-деньгах стрэддла для акции, которая торгуется по цене $40 с вмененной волатильностью 25% и экспирацией через 16 дней?
|
ПОСЛЕДСТВИЯ ФОРМУЛЫ СТРЭДДЛА
Вега (Vega)
Дифференцируя формулу по волатильности, мы видим
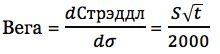
Получается, на-деньгах вега стрэддла является постоянной в отношении изменений волатильности. На-деньгах вега прямо пропорциональна времени до экспирации. Поэтому, по мере приближения срока исполнения опциона вега уменьшается.
Тета (Theta)
Дифференцируя формулу по времени, мы видим
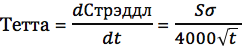
Таким образом, полученное выражение объясняет, почему тета на-деньгах опциона резко растет по мере приближения к истечению срока действия опциона.
Дельта и Гамма
Возможно, возникнет желание дифференцировать формулу относительно цены базового актива, чтобы попытаться найти дельта и гамму стратегии стрэддл. Однако обратите внимание на то, что формула рассчитана, что спотовая цена равняется страйку. Однако, чтобы определить гамму и дельту, спотовая цена S должна быть независима от страйка. В частности, неверно, что