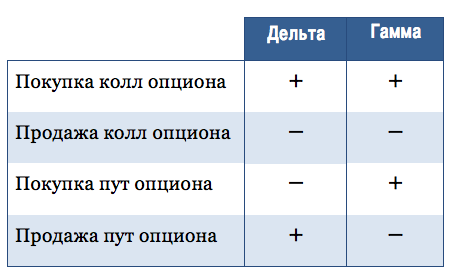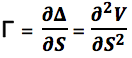
Δ – дельта опциона
V – цена опциона
S – цена базового актива
Математически, дельта является 1-ой производной цены опциона относительно цены базового актива. Гамма – это 2-ая производная относительно цены актива.
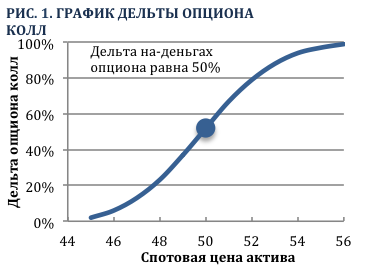
Гамма указывает на изменение дельты при движениях цены базового актива, т.е. с математической точки зрения гамма представляет производную от дельты опциона относительно цены базового актива. Рисунок 1 показывает, что дельта (коэффициент наклона касательной к графику цены опциона) не является постоянной величиной, а зависит от цены актива.
Дельта используется в качестве индикатора изменения стоимости цены опциона только при небольших изменениях цены актива и предполагает линейную связь между ценой базового актива и ценой опциона. Однако, если цена актива вырастет или упадет очень сильно, то фактическое изменение цены опциона будет существенно отличаться от того, на которое указывает дельта. Подробнее о дельте можно прочитать в Дельта опциона как коэффициент хеджирования – графики, формула.
Трейдеры опционов сравнивают дельту с дюрацией, когда рассматривают отношение между ценой облигации и процентными ставками, а гамму – с конвекцией.
|
Гамма Гамма (или конвекция, используя терминологию облигаций) измеряет скорость изменения дельты опциона. Гамма указывает на степень выпуклости (округленности) графика цены опциона относительно базового актива в определенной точке, где находится цена актива. Чем больше выпуклость графика, тем быстрее изменяется дельта.
Приобретение опционов колл и пут приводит к длинной (или положительной) гамме, а продажа опционов – к отрицательной гамма позиции. |
Гамма риск
Так как профессиональные участники рынка опционов используют дельту для управления риска своего портфеля, они подвержены риску изменения дельты позиции. В прошлой главе трейдер продал 1 тыс. колл опционов на акцию Газпрома с дельтой 0,50 каждый. Таким образом, дельта позиции составляет минус 500 акций. Другими словами, при небольших движениях цены акции прибыль (убыток) от короткой опционной позиции будет аналогична прибыли (убытку) от короткой позиции в 500 акций – не 1 тыс., так как изменение цены опциона колл составит половину от изменения цена акции.
Для хеджирования дельты, т.е. сокращения дельты до нуля, трейдер покупает 500 акций. Такой хедж будет эффективным только при незначительных колебаниях цены акции. Проблема возникает, если цена акции вырастет быстро и высоко, так как короткая опционная позиция понесет убытки значительно выше, чем показывает дельта. Такое поведение является следствием гаммы или конвекции. Прибыли от приобретенных 500 акций будет недостаточно, чтобы покрыть убытки от опционной позиции, так как цена акции обладает свойством линейности, а значение дельты изменяется в линейной пропорции.
|
Пример. В примере из статьи про дельту опциона, трейдер продал опционы колл на 1 тыс. акций с дельтой 0,50 каждый, что эквивалентно короткой позиции в 500 акций. Затем трейдер хеджирует дельту через покупку 500 акций. Гамма проданных опционов равна 0,01 или 1%. Это означает, что при росте (падении) цены Газпрома на 1% дельта колл опциона увеличится на 0,01. Дельта0 = Дельта опционов + Дельта акций Дельта0 = – 1000 x 0,5 + 500 = 0 Гамма0 = – 0,01 x 1000 = – 10 (Гамма имеет отрицательное значение, так как опционы были проданы.)
Шаг 1. Предположим, что как только трейдер продал опционы и купил 500 акций, цена акции поднимается на 10% и дельта колл опциона теперь составляет 0,60.
В таком случае, дельта короткой опционной позиции будет эквивалентна короткой позиции уже в 600 акций, а не 500. Теперь дельта всего портфеля не ноль, как было до роста цены, а минус 100 акций.
Дельта1 = Дельта0 + Гамма0 x 10% Дельта1 = 0 – 10 x 10% = – 100 акций
Это говорит о том, что трейдер потерял от опционной позиции больше, чем заработал от 500 акций.
Шаг 2. Дальше трейдер встает перед выбором. Во-первых, трейдер может оставить все как есть, т.е. продолжать держать 500 акций и надеяться, что цена акции упадет назад, и весь портфель скомпенсирует потери, так как дельта портфеля равна минус 100 акций. Заметим, что в случае дальнейшего роста цены акции убытки трейдера увеличатся, так как позиция не дохеджирована. Во-вторых, трейдер может купить дополнительные 100 акций с целью полного сокращения дельты до нулевого значения. Но если цена акции упадет назад дельта опционной позиции снова окажется минус 500 акций при длинной позиции в 600 акций. Следовательно дельта всего портфеля будет иметь положительное значение, и трейдер опять понесет убытки, так как при падении цены Газпрома дельта суммарной позиции будет увеличиваться из-за отрицательной гаммы. |
Пример наглядно показывает, что короткая опционная позиция приводит к убыткам при значительных колебаниях цены базового актива. Следовательно длинная опционная позиция должна приносить прибыль при существенных движениях базового актива при условии постоянного дельта хеджирования.
Гамма и денежность опциона
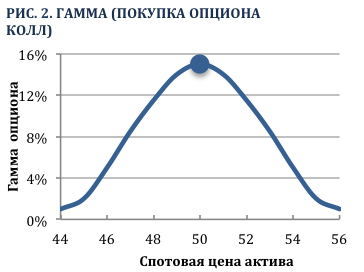
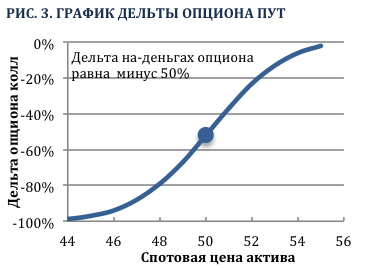
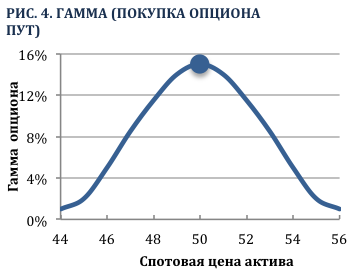
График на Рис. 1 (выше) изображает отношение межу дельтой колл опциона со страйком $50 и ценой базового актива. Дата истечения опциона наступит через 1 месяц. Заметим, что дельта подвержена более высоким изменениям, когда опцион находится на-деньгах, т.е. когда дельта равна 0,50 или цена базового актива составляет $50. Другими словами, дельта более чувствительна к изменению цены актива когда ее значениее составляет 0,50. Из этого следует, что гамма имеет наибольшее значение, когда опцион находится на-деньгах, что видно из Рис. 2.
Для сравнения, изменение дельты минимально, когда опционы колл и пут находятся глубоко в-деньгах или вне-денег. Дельта глубоко вне-денег опциона колл или пут практически равна нулю, т.е. вероятность исполнения опциона очень низкая. Таким образом, чувствительность к колебаниям цены актива тоже будет низкой. Поэтому гамма глубоко вне-денег опциона практически равна нулю. Для существенного роста дельты глубоко вне-денег колл опциона потребуется сильный рост цены базового актива, для пут опциона – сильное падение.
Глубоко в-деньгах колл опцион имеет дельту равную 1, что указывает на высокую вероятность исполнения опциона. Цена такого опциона движется почти один в один с ценой базового актива. Для существенного изменения дельты глубоко в-деньгах колл опциона потребуется значительное падение цены базового актива.
Гамма и дата исполнения
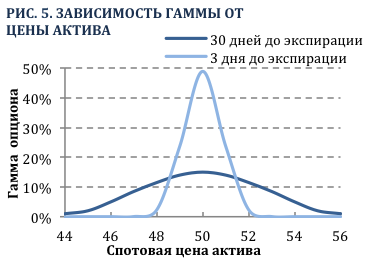
Рис. 5 изображает связь между ценой базового актива и гаммой колл опционов со страйком $50, но разными датами экспирации. На Рис. 6 можно увидеть, что гамма на-деньгах колл опциона возрастает по мере приближения к экспирации, в то время как гамма в-деньгах и вне-денег колл опциона падает. Из-за малого количества времени до момента экспирации увеличивается вероятность неисполнения вне-денег и в-деньгах опционов, дельты которых приближаются к нулю и единице (или минус 1 для пут опциона), соответственно. Чтобы в корень изменить ситуацию необходимо значительное движение цены базового актива. С другой стороны, судьба на-деньгах опциона характеризуется большей неопределенностью при экспирации через три дня, так как небольшое колебание цены базового актива способно сильно изменить дельту опциона, либо к нулю либо к единице (или минус 1).
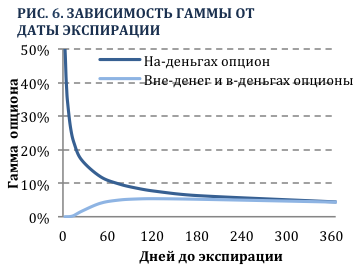
Такой феномен увеличивающейся гаммы для на-деньгах опционов, как колл, так и пут, имеет критическое значение для трейдера, который имеет короткую опционную позицию. Чем выше значение гаммы, тем более нестабильна дельта. Это приводит к более частому хеджированию дельты, и следовательно более высоким убыткам от ребалансировки портфеля.
Короткая опционная позиция заставляет трейдера хеджировать дельту себе в убыток путем покупки и продажи базового актива. При росте цены акции, продавец колл опционов должен покупать все больше акций, чтобы сократить дельту до нуля. Затем, если цена акции падает, трейдеру необходимо продавать купленные акции по более низким ценам, чтобы дельта опять была равна нулю. С другой стороны, держатель опциона (колл или пут) всегда будет хеджировать дельту с прибылью из-за положительной гаммы. Это означает, что дельта портфеля будет увеличиваться при росте цены актива, и снижаться при падении цены актива.
Тогда возникает вопрос, что отдает покупатель опциона взамен на положительную гамму (т.е. взамен на право хеджировать дельту с прибылью)? Ответ: тету. Опцион теряет временную стоимость по мере истечения времени (при прочих равных). С каждым днем стоимость опциона будет падать (при прочих равных) на величину теты. И если прибыль от хеджирования дельты за этот день окажется ниже значения теты, то трейдер в итоге понесет убытки. (Читайте также о Хеджировании дельты и гаммы портфеля опционов)