При торговле облигациями контрагенты обычно договариваются о цене. Из цены можно посчитать доходность бумаги, а затем спред над бенчмарком (государственная облигация с аналогичной дюрацией). Некоторые облигации с низким рейтингом котируются на основе кредитного спреда в базисных пунктах, как правило, кредитным спредом является Z-спред или G-спред.
Кредитные спреды, в свою очередь, являются функцией от степени возмещения (recovery rate) и вероятности дефолта. Поэтому, при заданном значении степени возмещения и кредитного спреда котируемой облигации можно определить вероятность дефолта. И наоборот, из предпосылок о степени возмещения и вероятности дефолта трейдер может рассчитать справедливую величину кредитного спреда и, впоследствии, сравнить ее с рыночной. Если облигация на рынке торгуется с более высоким спредом, чем показывают расчеты трейдера, то облигация торгуется дешево на рынке.
Вмененная вероятность дефолта: Простая модель
Рассмотрим облигацию, которая торгуется по номинальной стоимости, с доходностью к погашению 5% годовых. Доходность суверенной облигации с аналогичной дюрацией составляет 1%. Таким образом, кредитный спред облигации составляет 4% (5% минус 1%) или 400 базисных пунктов. Это означает, что инвесторы готовы недополучить 4% от номинальной стоимости облигации каждый год в случае дефолта. Если степень возмещения бумаги равна нулю, то вмененная вероятность дефолта составляла бы 4%. Однако, инвестор, основываясь на исторических данных, ожидает получить 40% от номинала в случае банкротства. В таком случае вероятность дефолта будет выше, чем 4%.
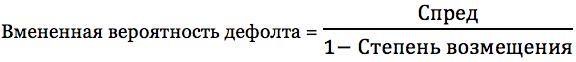
Вмененная вероятность дефолта = 4%/(1 - 0,4) = 0,067 = 6,7%
Из формулы следует, что вероятность дефолта облигации составляет 6,67% в течение одного года. Модель базируется на предположении, что инвестору должно быть безразлично, куда инвестировать: в суверенные облигации или корпоративные, так как кредитный спред должен компенсировать потенциальные потери в случае дефолта эмитента. На научном языке такая модель называется риск-нейтральной (risk neutral).
Вмененная вероятность дефолта: Детальная модель
Для разработки более детальной модели рассмотрим корпоративную облигацию с датой погашения через 5 лет, доходностью 4% и купоном 7%, который платится раз в полгода. Доходность суверенной облигации с аналогичной дюрацией и купоном равна 2%. Из доходности корпоративного облигационного займа, рыночная цена составляет $104,65, в то время как цена безрисковой бумаги составляет $119. Поэтому, ожидаемый убыток от дефолта эмитента равен $14,35 ($119 минус $104,65).
Предположим, что безусловная вероятность банкротства эмитента обозначается буквой P. В таблице ниже рассчитывается ожидаемая величина убытка при дефолте компании, выраженная в единицах P. Мы предполагаем, что кредитное событие может произойти в середине каждого последующего года). Также, допустим, что кривая безрисковых доходностей имеет плоскую форму, т. е. все безрисковые ставки по всем датам погашениям держатся на уровне 2%.
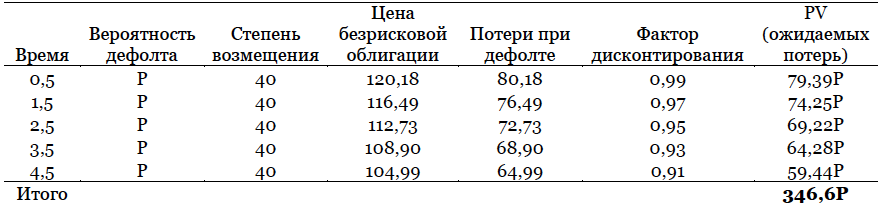
Продемонстрируем, как были получены значения в таблице на примере строчки 2,5 лет. В первом столбце указаны даты потенциального дефолта. То есть дефолт может произойти либо через полгода, либо полтора, либо 2,5, 3,5 , или 4,5 лет. Ожидаемая цена корпоративной облигации через 2,5 года за день до получения купона, при условии что дефолт невозможен, должна равняться цене безрисковой облигации:
3 + 3 x (1 + 0,02)-0,5 + 3 x (1 + 0,02)-1 + 3 x (1 + 0,02)-1,5 + 3 x (1 + 0,02)-2 + 103 x (1 + 0,02)-2,5 = $112,73
Если же дефолт имеет место быть, то инвестор получает только $40. Таким образом, в случае банкротства потери составят $112,73 – $40 = $72,73. Дисконтированная стоимость ожидаемых потерь:
$72,73 x 0,95 = $69,22
Следовательно, ожидаемый убыток составляет $69,22P. Совокупный ожидаемый убыток по всем годам равен 346,6P. Поэтому,
346,6P = $14,35
P= 4,1%.
Мы получили, что безусловная вероятность дефолта эмитента составляет 4,1%. Однако, в предыдущем примере было сделано много допущений, упрощающих исчисление вероятности дефолта. Мы предположили, что компания может объявить банкротство только один раз в год в середине года. Также, вместо использования безусловной вероятности, мы могли бы построить временную структуру вероятности дефолта, где на каждый отрезок времени используется отдельная облигация компании.
Например, для расчета вероятности дефолта в течение первых 3-х лет, используется трехлетняя облигация, для вероятности дефолта на 4-й и 5-й года используется 5-ти летняя облигация того же эмитента. Таким образом, вероятность дефолта имела бы временную структуру, т.е. зависела бы времени с текущего момента.
