Цена долговой ценной бумаги определяется методом дисконтированных денежных потоков. Процентная ставка, которая используется для нахождения текущей стоимости будущих платежей (или ставка дисконтирования) зависит от доходности по наиболее сравнимой облигации (с аналогичной дюрацией, кредитным качеством и рейтингом). В этом разделе мы разберем как посчитать справедливую цену обыкновенной облигации, не имеющей права досрочного погашения (call feature).
Обыкновенная облигация представляет серию будущих денежных потоков, включающих периодические купонные выплаты и номинал, который возвращается держателю облигации в дату погашения. Эта схема изображена в таблице ниже.
Денежные потоки обыкновенной облигации

С – купон в денежном выражении
N – номинал облигации
Справедливая стоимость облигации – это сумма текущей стоимости всех будущих денежных платежей. Все платежи дисконтируются по одной и той же процентной ставке r.
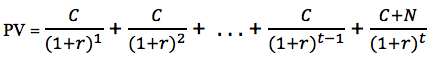
Облигация с годовыми купонными выплатами
|
Пример 1. Рассчитаем цену облигации с годовым купоном 7% (платится в конце года), с датой погашения через 3 года и номиналом 1,000 рублей. Доходность схожей по кредитному профилю облигационному выпуску составляет 5%.
Денежные потоки:
1) 3 купонные выплаты по 70 рублей, получаемые в конце каждого года 2) 1,000 рублей через 3 года. |
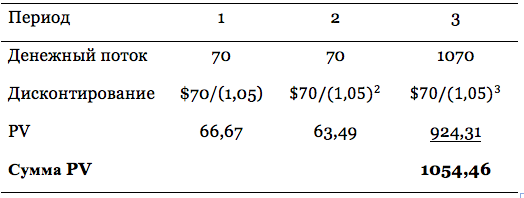
Облигация с полугодовыми купонными выплатами
|
Пример 2. Стандартная модель для определения цены облигации с полугодовыми купонными выплатами дисконтирует каждый полугодовой платеж по ставке, равной половине годовой ставки дисконтирования. Цена облигации – это сумма текущих значений всех платежей. Рассмотрим предыдущий пример, однако, теперь купон в размере 35 рублей будет платится в конце каждого полугодия в течение трех лет.
Денежные потоки:
1) 6 купонных выплат по 35 рублей, получаемых в конце каждого полугодия 2) 1,000 рублей через 3 года. |

Бескупонная облигация
|
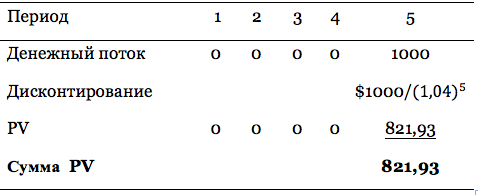
Пример 3. Найдем цену бескупонной облигации с датой погашения через 5 лет и доходностью 4%. В связи с тем, что облигация не платит купон, она как правило торгуется ниже номинала. Доход инвестора заключается в разнице между ценой покупки и номиналом. Если же реальные ставки в стране отрицательные, как в Германии, Швейцарии, Дании в 2014-2017 гг., то облигация будет торговаться с отрицательной доходностью. Денежные потоки: 1,000 рублей через 5 лет. |
Цена облигации между купонными выплатами
|
Пример 4. Предыдущие примеры продемонстрировали упрощенную методику расчета цены облигации, так как мы находили цену на первую дату купонного периода. В случае, когда необходимо определить цену облигации в середине купонного периода, требуется внести некоторые изменения в модель расчета цены, принимающие во внимание дневную конвенцию (например, 365/365).
Задача: рассчитать цену казначейской облигации США на 3 июля 2006 года, которая погашается 15 ноября 2007 года. Купонная ставка составляет 6% годовых и платится раз в полугодие: 15 ноября и 15 мая. Ставка дисконтирования равна 5%. |
Шаг 1. Найти количество дней в текущем купонном периоде. Последний купон был заплачен 15 мая 2006 года, а следующий будет 15 ноября 2006 года. Поэтому, текущий период содержит 184 дня.
Шаг 2. Найти количество дней с 3 июля 2006 г. до следующей купонной даты – 15 ноября. Оно равно 135 дней.
Шаг 3. Поделим 135 на 184, чтобы получить время до следующей купонной даты в количестве периодов (135/184 = 0,7337). Другими словами, следующий купон будет получен через 0,7337 периодов.
Шаг 4. Дисконтирование денежных потоков.
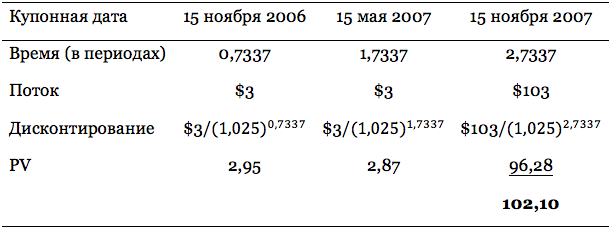
Накопленный купон = $3 x (49/184)= $0,8
Чистая цена = $102,1 – $0,8 = $101,3
Текущая стоимость всех денежных потоков, т.е. грязная цена, с 15 ноября 2006 года составляет $102,1. Эта цена отличается от чистой, в связи с тем, что мы приобретаем облигацию в промежутке между купонными платежами. В последний раз купон был заплачен 49 дней назад (15 мая 2006 года). Поэтому, накопленный купон составляет $0,8. Сумма накопленного купона $0,8 и чистой цены облигации $101,3 называется грязной ценой облигации ($102,1).
