В статье про синтетические форварды описывались ограничения по цене опционов и фундаментальный принцип, называемый пут-колл паритетом. Следующим логическим шагом в изучении опционов и модели ценообразования Блэка-Шоулза является построение бинарного дерева. Рассмотрим пример построения бинарного дерева, который базируется на допущениях, что базовый актив торгуется по цене $100 и может либо вырасти на 15% либо упасть в цене на 15% в течении одного периода времени, как нарисовано на Рис. 1 ниже.
Рис. 1. Одношаговое бинарное дерево
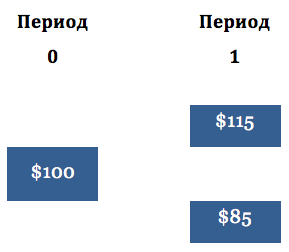
Допустим, что трейдер продает на-деньгах колл опцион, который истекает в конце периода 1. Цель трейдера заключается в определении справедливой стоимости колл опциона в настоящий момент времени (период 0). Назовем эту справедливую стоимость С. В период 1 цена опциона колл равна либо $15 либо нулю, что изображено на Рис. 2.
Рис. 2. Стоимость на-деньгах опциона колл
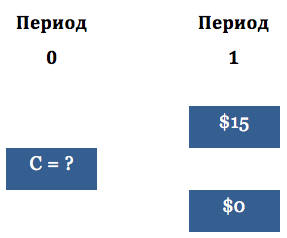
Цена опциона колл в период 0 может быть установлена путем вычисления стоимости хеджирования короткой позиции по опциону колл. Например, процентная ставка в настоящий момент равна 10%. Трейдер создает следующий портфель в период 0:
- продажа колл опциона и получение премии С
- покупка базового актива (количество акций равно дельте Δ опциона)
- приобретаем акции частично за счет получения премии С и привлечения кредита размером В под 10%
Получаем два уравнения:
(Δ x $115) – (B x 1,1) = $15
(Δ x $85) – (B x 1,1) = $0
Первое уравнение подразумевает рост цены акции на 15% до $115, и трейдер должен выплатить внутреннюю стоимость опциона $15 по короткому колл опциону. Чтобы трейдеру не уйти в убыток от выплаты $15, стоимость акций в портфеле за вычетом кредита и процентов должна составлять $15. Второе уравнение подразумевает падение акции на 15%, следовательно, цена опциона в период 1 равна нулю. Поэтому, цена акций в портфеле за вычитанием кредита и процентов должна составлять $0. При совмещении двух уравнений получается:
(Δ x $115) – (Δ x $85) = $15
Следовательно Δ = 0,5. Полученное значение 0,5 является дельтой опциона, также среди трейдеров называется коэффициентом хеджирования. Если трейдер продает колл опцион на определенное количество акций, трейдеру необходимо будет купить ровно половину акций для нейтрализации риска движения цены базового актива. Такой вид хеджирования называется дельта хеджированием, а результатом дельта хеджирования является дельта-нейтральная позиция.
Заметим, что дельту опциона можно напрямую посчитать следующим образом:
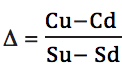
Cu – стоимость опциона при росте цены акции
Cd – стоимость опциона при падении цены акции
Su – стоимость акции при росте
Sd – стоимость акции при падении
В этом примере:
D = ($15 – $0) / ($115 – $85)= 0,5
Так как дельта опциона уже подсчитана, подставим ее в любое из двух уравнений, чтобы найти величину необходимого кредита для приобретения акции. Используя второе уравнение:
(Δ x $85) – (B x 1,1) = 0
(0,5 x $85) – (B x 1,1) = 0
B = $38,64
Остается последний шаг. Чтобы трейдеру не зафиксировать убытки в период 0, расходы на покупку акций (в нашем случае половины акции) в портфеле должны быть покрыты с помощью кредита В и полученной премии от проданного опциона колл. В нашем примере, дельта составляет 0,5 и объем кредита В составляет 38,64. Следовательно:
C + B = Δ x Спотовая цена акции
C + 38,64 = 0,5 x $100
C = $11,36
Формула расчета стоимости колл опциона
Вычисления стоимости опциона, показанные выше, можно сократить до одной формулы. Допустим:
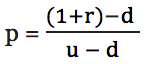
r – процентная ставка за один период (10%)
d – фактор, который снизит цену акции (0,85)
u – фактор, который повысит цену акции (1,15)
Из примера выше:
p = (1,1 – 0,85)/(1,15 – 0,85)= 0,83
Стоимость опциона колл С за одну акцию выражается следующим уравнением:
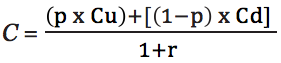
Cu – стоимость опциона при росте цены акции
Cd – стоимость опциона при падении цены акции
Следовательно:
C = (0,83 χ $15 + 0,17 χ $0)/1,1= $11,32
Заметим, что цена колл опциона рассчитана как среднее взвешенное значение и основана на идее, что риск от опциона можно полностью захеджировать. Из этих допущений следует, что вероятность роста акции до $115 к моменту экспирации (т.е. цена опциона достигнет $15) составляет 83%. В то время как вероятность падение акции до $85 (т.е. опцион обесценится) приравнивается к 17%. Среднее значение от двух потенциальных выплат, взвешенное на основе вероятностей осуществления каждого сценария, дисконтируется на один период назад по процентной ставке 10% для вычисления стоимости опциона в период 0.
Эти псевдо-вероятности широко применяются в академических исследованиях для описания риск-нейтральной среды, в которой риск от опциона может быть совершенно точно сведен до нуля через создание дельта-нейтрального портфеля. Очень важно не перепутать псевдо-вероятности с прогнозом аналитика относительно цены акции в будущем. Заметим, ожидаемая цена акции в период 1 из примера выше, чем $100, так как безрисковая процентная ставка находится на уровне 10%. Ожидаемая цена – это форвардная цена базового актива, которая рассчитывается как $100 х 1,1 = $110. Именно поэтому, вероятность роста цены акции до $115 (83%) значительно выше вероятности падения до $85 (17%).
