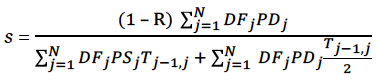CDS премия по облигации рассчитывается исходя из
- степени возмещения
- вероятностей дефолта
- безрисковых процентных ставок
При наличии всех компонентов можно определить справедливую величину CDS премии, используя безарбитражный подход. Такой подход подразумевает, что ожидаемая величина поступлений от продажи кредитного дефолтного свопа должна равняться ожидаемому значению выплаты в случае дефолта.
Рассмотрим два сценария:
а) нет дефолта

б) дефолт

где
s – CDS премия
T – количество дней между последним поступлением премии и дефолтом
R – степень возмещения
Шаг 1. Первым шагом будет определение текущей стоимости денежных поступлений от продажи CDS в случае, если дефолта не происходит:
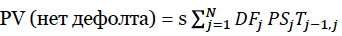
s – CDS премия
DF – фактор дисконтирования, рассчитываемый с помощью безрисковых ставок
PS – вероятность, что дефолт не происходит в определенный период (вероятность выживания)
T – длинна периода (измеряется в годах)
Шаг 2. Теперь необходимо найти величину денежных поступлений в случае дефолта. Если дефолт происходит в середине периода C, а покупатель CDS произведет платеж в конце периода C, то
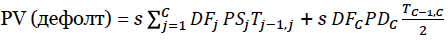
где
PD – вероятность дефолта в период C
R – степень возмещения
А платеж продавца CDS покупателю в случае дефолта составит:
(1 – R) DFcPDc
Формула расчета CDS премии
Безарбитражный подход, который также используется при определении справедливой фиксированной ставки процентного свопа, базируется на следующем аргументе: ожидаемая величина всех CDS премий должна равняться ожидаемому значению выплаты по CDS в случае дефолта.
В связи с тем, что дефолт может произойти в любой период получаем:
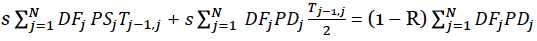
Первая часть выражения по левую сторону от знака равенства указывает на ожидаемую величину поступаемых платежей продавцу CDS, если дефолта не происходит, вторая часть – дисконтированное значение накопленной части CDS премии перед дефолтом. Правая часть равенства отражает ожидаемое значение величины, которую должен возместить продавец CDS контракта покупателю в случае дефолта.
При переставлении выражений из равенстве получаем, что премия по CDS составляет