Безусловно, бинарное дерево, которое было построено в статье “Бинарное дерево (Часть I)”, является упрощенной формой реальной опционной модели, используемой в инвестиционных банках. Базовая модель предполагает, что цена акции либо возрастет до $115 либо упадет до $85 в течение одного периода. На практике, во-первых, цена актива растет и падает мелкими шагами, выстраивая со временем целую динамику движения. Во-вторых, факторы u и d, изменяющие цену акции от спотового значения, используются лишь для иллюстрации. В реальности, разработчики опционных моделей пытаются вывести наиболее подходящие значения для этих факторов путем вычисления волатильности цены акции. Из логических соображений следует, что при прочих равных более высокая волатильность базового актива приведет к большему отклонению цены от текущего уровня, и, следовательно, к более высокой стоимости опциона.
Чтобы показать, как можно решить вопрос с волатильностью, в этой главе мы построим 3-х шаговое бинарное дерево для нахождения справедливой стоимости европейского опциона на акцию, которая не платит дивиденды.
Спотовая цена акции S = $300
Цена исполнения опциона X = $250
Безрисковая процентная ставка r = 10% годовых
Время до экспирации t = 0,25 лет
Волатильность σ = 40%
Для построения дерева, которое бы сопоставляло волатильность базового актива с факторами u и d , мы будем использовать следующие формулы, предложенные американскими академиками Коксом, Россом и Рубинштейном в 1979 году:
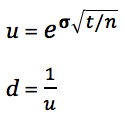
e – математическая константа (приблизительно равна 2,71828)
t – время до погашения опциона в годах (0,25 лет или 3 месяца)
n – количество шагов бинарного дерева (три шага)
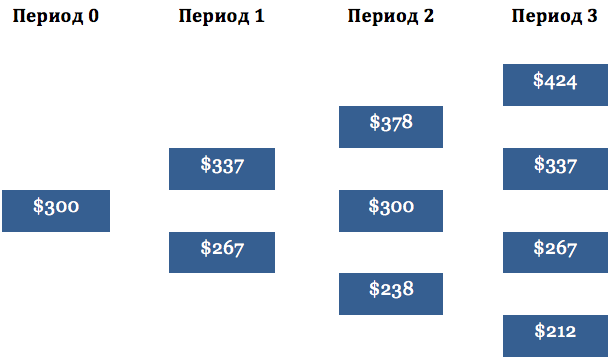
Рис. 3. Трехшаговая модель бинарного дерева
Рассчитываем u и d:
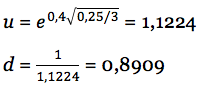
Общее время действия опциона делится на три равных периода. Рисунок 3 показывает, как значения u и d используются для построения бинарного дерева. Например, первое движения цены актива вверх, имеющее значение $337, полученное путем умножения $300 на величину u. Значение $267 рассчитывается через умножение $300 на величину d. Если цена акции достигает значения $267 в период 1, она может либо увеличится до $300 в период 2 ($267 умножить на u), либо произвести дальнейшее падение до $238.
Построение дерева для колл опциона
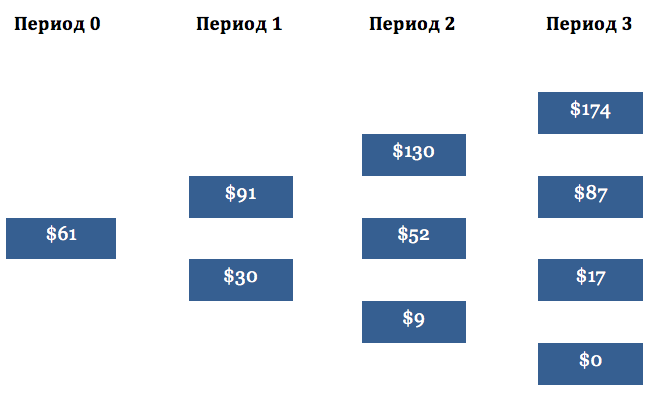
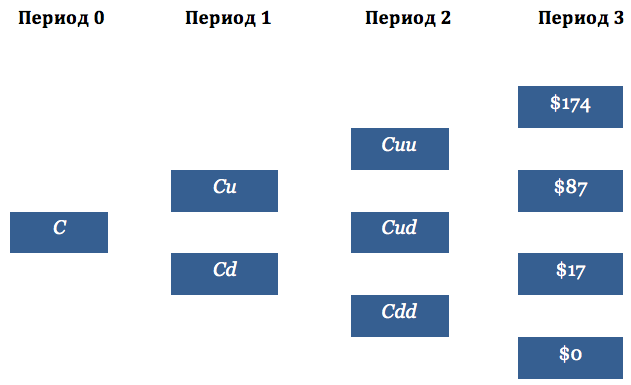
Следующим шагом является построение дерева, которое представляет стоимость колл опциона со страйком $250, исходя из динамики движения цены акции. Легче всего начать с конца – в момент экспирации стоимость колл опциона определяется исключительно внутренней стоимостью опциона, как показано на Рис. 4. Например, в верхнем правом углу дерева цены базового актива на Рис. 3, цена акции составляет $424. В таком случае, колл с ценой исполнения $250 будет стоить $174.
На Рис. 4 буква C изображает стоимость опциона в период 0. Cu – цена опциона при росте цены акции на один уровень; Cuu – цена опциона при росте акции на два уровня. Cd – цена опциона при падении акции на один уровень, Cdd – цена опциона при падении на два уровня; Cud – цена опциона при росте акции на один уровень и последующем падении на один уровень.
Рис. 4. Трехшаговое дерево для колл опциона
Стоимость колл опциона в каждый период может быть получена путем разделения трех-шагового дерева на три дерева с одним шагом для простоты вычислений. Для начала необходимо посчитать вероятности p и (1 – p), используя факторы u и d.
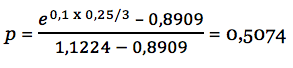
1 – p = 0,4926
Cuu равняется дисконтированному значению от суммы: 1) колл опциона при росте акции до $424 (т.е. $174) умноженной на вероятность роста акции до $424 за период и 2)колл опциона при росте акции до $337 (т.е. $87) умноженной на вероятность роста акции до $337 за период.
Уравнение выглядит следующим образом:
Cuu = [($174 x 0,5074) + ($87 x 0,4926)] x e-0,1 x 0,25/3 = $130
Завершенное трехшаговое бинарное дерево изображено на Рис. 5. Текущая справедливая стоимость колл опциона со сроком погашения через три месяца приблизительно составляет $61. Если бы мы находили стоимость американского пут опциона, было бы критично проверять на каждом шагу, чтобы цена не падала ниже внутренней стоимости опциона. Такая ситуация возможна в связи с тем, что американский пут иногда выгодно исполнять заранее.
Рис. 5. Трехшаговое дерево для колл опциона